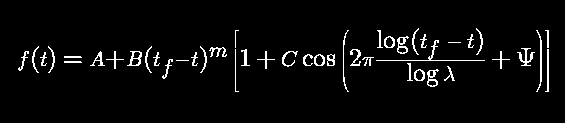タイトル：地震は大地の摩擦である

古来、地震は地中に住むナマズのみじろぎによって引き起こされるとされてきた。勿論、いまではそんなたわごとを信じている人は殆どいないだろうけれども、では、地震がナマズの仕業と思われていた時代に比べてどのくらい地震が科学的に理解されたかというと、正直なところ、あまり、解っていないのだ。今回のインタラクティブ・サイエンス・コラムは、近年行なわれている物理学者による研究の現状を見てみよう。

今年の一月に神戸で起きた大地震の被害は辛酸を究めた。最初の報道を聞いた時に数千人単位の死者が出ると予想された方々は専門家を除けば、少なかったのではないか。この様な惨状に対して物理学者ができることはほとんど無い。実際、物理学者は世の中のためになることは殆ど出来ない。だが、それでも、物理学者なりに地震現象を理解しようという努力はなされており、特に、ここ１０年ほどはかなり盛んに研究がされるようになった。

と言っても、物理学者にできることはおのずと限界があり、現実の地震を相手にした地震予知などそうそうできない。で、物理学者が最初に目的としたのはグーテンベルク-リヒター則という「大きい地震は滅多に起こらず、小さい地震はたくさん起きる。その頻度の比はどうなっているか？」ということに関する４０年近く前から知られているが理由が謎のままの法則を再現することであった。そのために、物理学者は地震現象を非常に単純化・理想化したモデルを構築することから始めた。このモデルの最も基本的な仮定は「地震は要するに地面の摩擦で起きているんではないか」ということだった。なんだか嘘臭いが、これでも結構グーテンベルク・リヒター則は再現されてしまったのである。だから、少なくとも、このモデルは地震の起きる頻度をうまく説明できるモデルになったわけだ。

と、なると、今度は、「では、予知ができるか？」という問題になる。地震のうまいモデルになっているなら、まず、このモデルで「予知」をしてみようということだ。「自分で作ったモデルで予知も何もないではないか。いつ、大きな地震が起きるか分かるに決まっている」と思うかも知れないが、全然、そうではない。まず、現実の観測では、過去に起きた地震の記録があるだけだから、このモデルで「予知」をやる時にも、過去のデータ、つまり、どのくらいの地震がいつ起きたか、というデータだけを与えることにする。これで、地震を予言できるだろうか？結果は残念ながらNoであった。過去において殆ど同じような地震の起き方をしていてもある時は地震が起き、また、ある時は地震が起きないという風になってしまった。これは、現実の地震でも良くあることで「事後予知」と呼ばれている。こういう困った性質まで再現してくれて、物理学者としては非常に面白いのだが「予知」の役には全然立たない。実際、冷静に考えてみると、過去にどういう地震が起きたか、という情報だけで、このモデルの地震を予知できるとはとても思えないのである。

現実の地震予知では、過去の地震の記録だけでなく、周囲の様々な観測を通じて総合的に地震を予知しようとしているわけだから、例え、このモデルが本当に地震のモデルだとしても、このモデルで予言ができないからといって、現実の地震予知ができないということには全然ならない。だが、「他のいろいろの観測を用いる」ということは、情報を増やす＝おもりの一つ一つの動きを見る、という方向にどんどん近付いているわけだ。もし、そうしなくてはならないなら、機構の良く解っていない地震の予知をするのは大変、難しいことになる。
どうも、暗い話しばかりしてしまったので、ちょっとは明るい話しもしておこう。最近、ある物理学者は、「大地震の前のある観測量の変化はこうなるはずだ」という式を導出した。妙に簡単な式だが、良くあっているようだ。これが過去に起きた大地震に対してではなく、未来におきる大地震の予知に役立つことを願って、終りにしよう。

物理学者ができることはほとんど無い
とは言うものの、日本における地震研究の一大拠点、東京大学地震研究所を設立したのは、関東大震災の惨状に激しい衝撃を受けた物理学者、寺田寅彦であるらしい。当然、寺田が望んだ科学的成果の一つは地震予知である。

寺田寅彦
（１８７８－１９３５）
科学者としての業績よりも、もっぱら、「随筆集」の著者として、また、夏目瀬石の出世作、「我輩は猫である」の寒月先生のモデルとしてばかり有名だが、戦前の日本の物理学会（当時は数学会と一緒）では重鎮ともいうべき有力な科学者だった。彼が晩年に行ない、「随筆集」に描写した「身の回りの科学に注目する」という研究方針は、当時の新興科学である量子力学のブームに押されて決して主流になることはなかったが、現代、カオス、フラクタル、と名付けられて盛んに研究されている分野には彼の興味とオーバーラップする部分が極めて多い。

地震予知
さて、例によって、全然、専門家でないのだが、それでも、地震予知の困難についていささか述べておこう。まず、第一の問題は、地震の機構がちっとも解っていないことだ。第２の問題は、地震予知そのものの有効性だ。この２つの問題があるために寺田の時代から半世紀以上経っているにも関わらず、地震予知の科学には本質的な進歩が見られないのである。

専門家でないのだが
といいつつ、卒業論文は地震予知の研究室で書いてたりする。指導教官だった先生、ごめんなさい。出来の悪い弟子をお許し下さい。

地震の機構

勿論、ナマズの時代から比べれば解っていることは多い。ウエゲナーの大陸移動説で知られているように地球の大陸は動いている。動いていればゆっくりとではあるがお互いに衝突する。衝突すれば、衝撃で振動が起きる。これが地震というわけだ。だが、実際に衝突すると言っても、現実に衝突が起きているのは何十キロという地中深くである。これほど、深くなると温度も数百度、圧力もすごく高いというとんでもない条件になっている。この様な条件下で岩石がどの様に振舞うかと言うのは実は良く解っていない。実験が出来ないこともないが、なにしろ、実際の巨大な岩石のサイズの実験は難しい。そうなると、肝心の運動がよく解らないので、地震の機構を完全に理解することなど最初から不可能なわけだ。この困難をうち破るために地中深くボーリングを行なって地震が生じている領域に少しでも近付こうと言う試みがなされているが、まだまだ、ゴールは遠いのが現状だ。

衝撃で振動が起きる・殻と殻・卵と殻の例え
もう少し詳しく説明すると、動いているのは大陸そのものではなく、地球の表面そのものが動いている。例えて言えば、ゆで卵の殻にひびが入っていて殻が数枚のかけらに分かれている。そして、それらがお互いにぶつかりながら動いている、というイメージである。地球の表面は凸凹しているから大きく出っぱっているところ（＝高い所）が海の上に出て大陸になっているわけだ。殻が動くと大陸も動くので、我々には大陸が動いているように見えるわけだ。
さて、ぶつかった殻はどうなるか？大体はどっちかがどっちかの下にもぐり込むことになる。もぐり込む時に摩擦があるのでもぐり込まれた方は引っ張られる。しかし、殻はそれなりに固いので、引っ張られるのには限界があり、そのうち、いつかは戻ろうとする。この「戻り」が地震である。

（図０）

この様な理解が標準的な理解だが、ごく最近、地震は専門外の研究者が全然別のシナリオを提出した（「ながれ」（日本流体力学会誌）１９９５年８月号３０５頁）。殻は本当は固くなくて非常にゆっくりとだが水の様に流れることが出来るとする。そして、片一方の殻がもう一方の殻の下に「流れ込む」という計算を行なうと、やはり、地震のような振動が生じうる、という研究だ。これだと、「固い殻」を想定した今までのモデルと根本的に違うものになってしまう。この論文は門外漢によって書かれたものだし、挙動の分かっていない地中の岩石の運動を液体と仮定して出した結論だから、地震の専門家に簡単に受け入れられるとも思えないが、とにかく、地震の理解とは基本的なことさえ、この程度なのである。

ウエゲナー
（１８８０-１９３０）
大陸が動いていることにいち早く気付き「大陸と海洋の起源」（昔は岩波文庫の青帯に入っていて簡単に手に入った。今はどうだろうか？おもしろい本だった。）という大著を出版したが、認められることなくこの世を去った。彼の時代にはプレートテクトニクスなどという考え方は無かったから、大陸の移動を別の理由で説明しなくてはいけなかった。ウエゲナーは地球の自転による遠心力などを考えたようだがその程度の力では大陸の移動を説明できなかった。いくら正しいことを主張しても、証明できなければ仕方が無い、といういい例であろう。ちなみに、５０才の若さで亡くなっているが死因は学術的探検（冬期のグリーンランド探検）の失敗であるらしい。頭がいいだけでなく、根性もあったらしい。

プレートテクトニクス
地球の表面の運動について、もっとも一般に受け入れられている理論。卵と殻の例えでいうと、白身が運動するのでそれにひきづられて、殻が運動する。この「白身」の部分はマントルと呼ばれていて、非常にゆっくり流れる液体の様なものだと思われている。地球の真中は熱いので、マントルが熱せられて膨張し、軽くなって上昇し、地表で冷やされてまた沈んでいく。これが大陸移動の原動力であると信じられている。もっとも、地球中心の発熱がマントルを対流させるのに十分な力を出せるかどうかを実際に計算した例は私は知らない。

大陸移動説
大陸が移動することが知られていない時代にはいろいろ説明できないことがあった。例えば、遠く大西洋を隔てた南米の東側とアフリカの西側に同時期に同じ種類の化石が見つかることなど。化石になった生物が生きていた時代、アフリカと南米は一つの大陸だったから、これはあたりまえだが、かつては大きな謎であった。細い地峡でつながっていたなどと、諸説あったが、大陸移動説はこのような困難をきれいに説明できる理論だった。地図を見れば分かるようにアフリカの西海岸と南米の東海岸はちょうどジグソーパズルのようにきれいに一致するのである。
この他にも、ウエゲナーの時代（１９３０年以前）に大陸移動説を裏付ける間接証拠はいろいろ出ていた（竹内均訳、原著第４版、講談社）。天文学的な観測、電話線を通って信号が大陸間を往復する時間、無線の電波が大陸間を往復する時間などから、大陸移動の速度を実測しようという試みさえあった。ただ、これらは今の観測精度からすると大雑把で、間違っていたようだ。間違っていたが、大陸移動説を指示する結果（つまり、多き過ぎる値。当時の観測では最大一年に数十メートル動いたことになっていた。今の常識では数センチである。）が出ていた。海底の深さや地表の高さが世界中どこでも大体同じであるということも、大陸移動説の根拠になっていたようだ。軟らかい「白身」の上に固い「殻」が乗っているという構造であれば、高過ぎる山は沈んで低くなってしまうからだ。古代の気候に関する議論も用いられた。南アフリカが昔は氷に覆われていた、などということは大陸移動説がもっともうまく説明できるからだ。更に、すごいことに、大陸が移動することにより、地球の地軸がゆがむ可能性にもウエゲナーは気付いていた。地球は宇宙で回るコマのようなものだから、表面でものが移動すれば当然、回転は不安定になる。安定してまわっているコマの一ヶ所に粘土の固まりを付ければグラグラするのと本質的には同じである。
この様な議論から解るように、大陸移動説は多分に学際的な分野だった。生物学、地質学、測量学などの総合的な知識が必要だった。大陸移動説が認められなかった最大の理由は勿論、大陸移動の機構を説明できなかったことだが、もう一つの理由はこの学際的な学問の性質にもあったのだろう。各々の分野には権威がいて、その分野だけを考えれば、大陸の移動を持ち出さないといけないほど大きな矛盾はなかったのだろう。しかし、全部の小さな矛盾を合わせると大陸移動説は俄然、説得力を増してくる。特定の分野では優れていても視野の狭い、頭の固い学者の説得に苦労しているウエゲナーの姿が目に浮かぶようである。
ちなみに、グーテンベルク・リヒター則のグーテンベルクは大陸移動説に反対だったらしい（少なくとも、ウエゲナーが生きているころは）。「大陸と海洋の起源」に、グーテンベルクは敵対者として登場する。グーテンベルクがグーテンベルク・リヒター則を発見するのはウエゲナーの死後、３０年近くたってからである（まあ、同名異人という可能性もあるけど）。

有効性

「有効性って何？予知できればそれでいいじゃん」と思うかも知れないが話しはそれほど簡単ではない。地震予知とよく比較される天気予報の例を見れば分かるように、予知には「正確さ」と「どこまで未来を予知できるか」という２つの要素がある。正確さとは、いつ起きるか、とか、どのくらいの規模か、という問題。天気予報なら、雨がいつ、どのくらい降るか、という問題だ。天気予報ではこの辺をうまく折り合いをつけて「××ミリ以上の降雨が朝６時から正午までにある確率は○○パーセント」とかいうわけだ。どこまで未来を予知できるか、という問題は短期予報、長期予報、とかいう区別である。一般に、長期予報ほど正確さは落ちていく。地震予知の場合はこれが大きなネックになる。ちょっと考えてみよう。あなたがテレビをつける。朝のニュースが始まる。天気予報に続いて地震予報である。「本日の地震予報です。今日の午後３時から６時までの間に阪神大震災クラスの地震が起きる確率は９０パーセントです。」...........さて、あなたはどうするだろうか？時刻までに危険地帯の住民を全部退避させるだけの輸送力はない。パニックが起きて地震そのもの以上の人命が失われるかも知れない。しかも、９０パーセントだから、１０回に一回は地震が起きないのだ。もし、起きない方の１０パーセントだったら、パニックで失われた人命は誰が責任をとるんだろうか。このような予報は明らかに殆ど役に立たない。役に立たせるには、耐震シェルターを町中に作っておき、予知されたらみんながそこに避難するとかすればいいが、もっと長期予報が望ましい。では、どういう長期予報が役に立つだろうか？天気予報の長期予報はこの程度だ。「今年の夏は冷夏でしょう。」では、地震予報は？「今年の夏は関東地方に阪神大震災クラスの地震があるでしょう」さて、これはどの様な役に立つだろうか？夏の間中、関東地方の４０００万の人々がどこかへ避難することが出来るだろうか？出来そうもない。大体、どれくらいの人が避難するか怪しいものだ。最初は避難するかも知れないが、１カ月経っても何もなかったら、かなりの人が舞い戻るのではないか。そこで地震が起きれば悲惨窮まりないだろう。１０数年前に中国で地震を予知したとして大騒ぎになったが、その実体は精度が１カ月程度で、その一カ月の間、住民は家に入らず、外で寝起きしていたらしい。こんなやり方は社会主義経済だからこそできることで、日本は勿論、今の中国ですら実施は不可能だろう。
天気予報なら、朝、傘を持って出るかどうかの判断ができればOKだから、２４時間前の予報で十分だ。だが、地震の場合、どの程度の精度でどれくらい前から予知すればいいのか、はっきりしないのだ。この点の議論はどの程度防備を固めるか（地震シェルターをつくるか、とか）と表裏一体の問題で難しい。

モデルを構築する・嘘臭いモデル・モデル
物理学者が地震のモデルと称して研究しているのは、このような物だ。

（図1）

これは、地震の機構の中でも、殻と殻衝突する部分だけをモデル化したものである。上の板がもぐり込まれる方の殻、下の板がもぐり込む殻、というわけだ。板ばねと殻同士の摩擦によってらせんバネが引き延ばされるが、ある程度バネが伸びると摩擦で支え切れなくなってどれかのおもりがバネに引かれて戻る。すると、動いたおもりの回りのおもりも引きずられて動く。すると、その回りのバネも...........と言う風に連鎖反応的におもりが動く。一度に多くのおもりが動くこともあるし、２、３個しか動かないこともある。この動いたおもりの数が多ければ大地震、少なければ、小さな地震、というわけだ。

グーテンベルク-リヒター則
話しが難しくなるが、ちょっと、つきあって欲しい。グーテンベルク・リヒター則では

「地震の生じる頻度は地震の大きさ（＝エネルギー）の冪乗の逆数に比例する」

つまり、エネルギーの２乗に逆比例するとするとエネルギーが１０倍大きい地震は１００回に一回しか起きない、というわけだ。マグニチュードが１違うと地震のエネルギーは３０倍違うので、起きる回数はずっと減ってくる。最近、「地震を予言した」という話しが良く週刊誌に載っているが、これは眉唾ものである。良く読むと、大体、予言に成功しているのはマグニチュード５クラスの地震で、阪神大震災に相当する７クラスの地震の１００００倍くらい起きやすい地震である。それで、地震を予言した主張するのは、「明日の天気があてられた。だから、一年に一回しか来ない巨大台風がいつ来るかも分かるぞ」といっているほどの（それよりまだひどい）論理の飛躍なのである。

「事後予知」
事後、とは物事が終った後、ということ。予知、とは物事が起きる前にすること。だから、事後予知、というのは言葉の矛盾だが、次の様なことを指す。「○月×日に大きな地震があった。記録を調べるとその寸前に奇妙な信号が記録されており、これが前兆現象だったことが解る。」つまり、ことが済んでから、前兆を見つけるから事後予知である。それなら、今回は駄目でも次回は気をつけていればいいだろうと思うかも知れないが、事後予知の困ったところは、そっくりな「前兆」を観測しても本震である大きな地震が結局来ないことも良くある、ということである。

冷静に考えてみる
このモデルで大きな地震が起きるのはいろいろ偶然が重なって、たくさんのおもりが滑べるか滑べらないかのぎりぎりの状態にたまたまなって、それから一斉に滑べる、という時しかない。さて、こういう状態になるためにはかなり長いこと、中くらいの地震（つまり、全部が滑べるわけでないが数個よりはずっと多くのおもりが一斉に動く）が起きない、という状態が続かなくてはならないだろう。なぜなら、そのような中くらいの地震があっちこっちで起きていては、全体のおもりが全部滑べるか滑べらないかというぎりぎりの状態に揃う前に、部分的におもりが動いてしまうからだ。では、中くらいの地震がずっと起きないためにはどうすればいいかというと、それよりやや小さい地震がかなり長いこと起きないでいなくてはならず、そのやや小さい地震が起きないためには............とやっていくと結局、将来、大きな地震が起きるかどうかは、今の時点でたった一つのおもりが動く小さな地震が起きるかどうかで変わってしまうということを意味する。こんな微妙なことに影響されては、遠い未来の地震の予言などできっこないモデルになっていることがわかる。

グーテンベルク・リヒター則は再現されてしまった
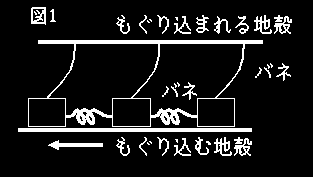
じつはこれには後日談がある。このモデルは地震を単に摩擦現象としてモデル化したのだから、見るからに摩擦のモデル然としている。逆にいうと、グーテンベルク・リヒター則は、実は地震の法則でもなんでもなくて、摩擦の法則なんではないか？こう思うのは僕一人ではないらしく、最近、ある実験家が次のような実験を行なった。

（図2）

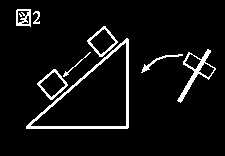
斜面の上に溝を掘ってアクリル棒をおく。斜面の傾きは滑り出すか出さないかギリギリくらいにしておく。次に、この斜面に衝撃を与える。すると、アクリル棒は滑り出すが、斜面の下まで滑べり降りてしまうわけではなく、どこかでとまる。この滑べった距離を「地震の大きさ」にみたてて統計をとると、見事にグーテンベルク・リヒター則を再現してしまった。何のことはない、やっぱり、摩擦の法則だったわけだ。

式を導出した
それは

（式）

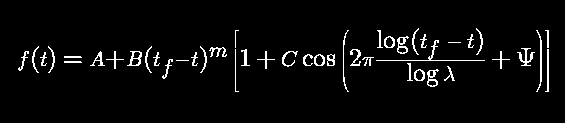
式の説明：tが時間（今の場合は年）。A,B,C,m,λ,Ψ,は定数。t_f(=1990年)に地震が起きた。

である。目の回るような式だけれども、地震のような複雑な現象の再現式としては極めて単純である。

（図3）

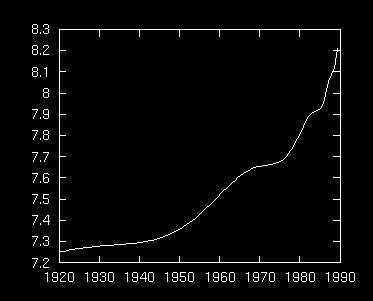
奇妙にクネクネしたグラフだが、これで観測を再現し、「事後予知」にも成功したらしい。次回の大地震の予知に是非活用して欲しいものだ。
更に、つい、昨日、この論文に関連した論文で

「地震予知に使われたこの式で株の大暴落も予知できる」

という論文が投稿された。ここまで行くと日本の三流週刊誌も真っ青だが、再現性は非常にいいようである。ただし、これを信じて投資して、破産してもインタラクティブ・サイエンス・コラムは一切、責任を取らないのでそのつもりで。