
この様子を目で見るのは実に難しいのだが、幸いなことに現在はコンピュータシミュ レーションでこの様子を目で見ることができるようになった。きれいなカーブを描く ひび割れの場合に、ガラス板にかかっている力の大きさを色で表現した コンピュータグラフィックスを見て欲しい。弱い力でゆっくり壊せば、破壊だって きれいなパターンを作り出せる。そして、実際、それはある時には「奇景」と言われ るみんなが金を払って旅行してまで見に来る すばらしい景観を作ることもある。 (ムービー提供:東北大学電気通信研究所/早川美徳(はやかわ よしのり)
柱状節理 (?)のムービー:
斜めから見たところ
Crack_3D-1.qt.hqx:
Crack_3D-2.qt.hqx:
Crack_3D-4.qt.hqx:
Crack_3D-5-long.qt.hqx:
Crack_3D-6.qt.hqx:
上から見たところ
D-longcolumn-top.qt.hqx:
Crack_3D-5-topview.qt.hqx:
Crack_3D-7-topview.qt.hqx:
(ムービー提供:東北大学電気通信研究所/早川美徳(はやかわ よしのり)
ゲルをゆっくり手で引き裂いたときに割れめにできるウロコ状の模様。
特に注意深くしなくても、また、実験用のゲルでなくてその辺で売っているゼリーと かでもゆっくり引き裂けば、こういうきれいなウロコ状の模様が出せるはずだ。暇だ ったら、やってみよう。このようにゆっくりやれば「破壊」という現象は我々にいろ いろ「秩序」を意味する「模様」を見せてくれるのだ。 ちなみに「手でさっと」引き裂くと割れ目にはきれいなウロコの模様ではなく、お 馴染みのぎざぎざが現われる
ゲルをさっと手で引き裂いたときに出来る割れ目の上のぎざぎざ。
ちなみに、この「ぎざぎざ」は、鋼鉄をすさまじい力で引き裂いたときにできるぎざ
ぎざ模様と良く似ている。硬いものも柔らかいのも「音速=力の伝わる速さ」で「速
く」引き裂けば同じ様な模様を残すというのは面白い。鋼鉄を「ゆっくり」引き裂く
ことが出来れば、逆に、ウロコ状の模様が出来るんだろうか、ひょっとして。
写真提供:京都大学基礎物理学研究所、教授関本謙・同大学院生中沢初美。
衝撃が加わったばかりのときは衝撃波の力は強く、物質を粉々に破壊できる。ところ
が、物質中を伝播して行くうちに衝撃波のエネルギーは物質の破壊に使われて消耗し
だんだん弱くなって行ってしまう。その結果、あまり粉々に破壊することはできなく
なり、かけらは大きくなっていく。かけらが大きくなれば当然、かけらの数は少なく
ならざる終えない。衝撃波の先端の面積はいつも同じだからだ。こういう議論を数学
的にきちっとやると、「
五乗して立方根をとる」とかいうかけらの数の法則が導き出せる。
2×破壊する物質の次元(立体なら3、板なら2、棒なら1)-(破壊領域の体積が
伝播距離の何乗かという数)
で、決まる。普通は、立体を壊し、破壊領域の大きさは伝播距離に比例して大きくな
るので伝播距離の1乗、ということなので2×3-1=5、になる。
これがどうしてかって?うーん、もう口で説明するのはちょっと難しい。
御免なさい。
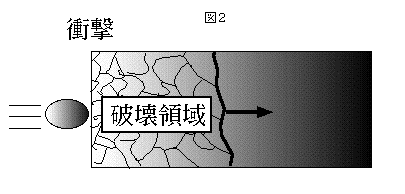
衝撃波で崩壊する物質
A2:必ずしも同じではないことは、A1:からもなんとなく解るだろう。衝撃波が外
からではなく中から加わったときなど、衝撃波の伝わる面の大きさが物質中を伝播す
るに従って広くなって行ってしまう。そうなると、衝撃波が弱くなるのと同時に一度
に破壊しなくてはいけない面積も増えて行くから、かけらはますます大きくなってし
まう。その結果、どういう重さのかけらがどれくらいあるか、という部分は変わって
しまう。その他、立体を壊すか、板を壊すか、棒を壊すかで、みんな結果は変わって
くる。 もっともっと詳しく
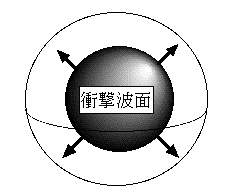
内部からの破壊。衝撃波の面積がだんだん広くなる。
もっともっと詳しく
あー、あなたも好きですねー。話がどんどん難しくなりますよ。いいんですか?
まず、
五乗して立方根をとる、の「立方根」の方、これは立体を壊すか、板を壊すか、棒を壊
すかで変わってくる。立体なら立方根、板なら平方根、棒ならそのまま、である。懸
命なる読者の方々ならこれが物質の「次元」に関係していることに気付かれるかもし
れない。立方根とはつまり、3回掛け合わせてその数になるような数を求めろ、とい
うことだ。平方根ならこの「3」が「2」になる。一方、物質の「次元」は立体なら
3、平面なら2、棒なら1、である。つまり、
五乗して立方根をとる、の立方根の部分は「物質の次元」という値で決まってくる
のである。
次に、
五乗して立方根をとる、の「五乗」の方だが、この五、の方は今度は衝撃波の伝
わり方によって決まってくる。衝撃で壊された領域の体積が衝撃波の伝わった距離と
ともにどう変わるか、に関係している。具体的には破壊領域の体積が衝撃波が伝わっ
た距離の何乗程度の大きさか、ということによっている。内部からの破壊の場合、破壊された領
域の体積は球形であるから、伝播距離の3乗で大きくなる。一方、普通の
場合、破壊領域の大きさは伝播距離に比例して大きくなるので伝播距離の1乗、とい
うことになる。
で、 五乗して立方根をとる、の五、とどうかんけいするかというと、この部分は
宇宙にまで及んでいる
アステロイド・ベルト、あるいは、小惑星帯、というのを知っているかな?火星と木
星の間に横たわる、小さな岩のかけらの集合体だ。この小惑星の重さの分布は「もの
を普通にハンマーなどで激しく叩き壊したときに見られる」とほぼ同じなのだ。だから、小惑星帯ってのは、何かが壊れて出来たもので
あり、その壊れ方は大きさの違いにも関わらず、ガラスの靴や冷凍ポテトと変わらな
いってことだ。物が壊れるってことひとつをとってみても、よく見てみれば宇宙のロ
マンとつながることもある。これがカガクの醍醐味なんだ